Making the Science Exact: Recent Developments in Cosmology
A. Kashlinsky
Cosmology is the study of how
the current structures in the Universe came about. Except for
some rare and speculative attempts, it does not try to answer how the Universe
itself came about but, rather, what were the physical processes that have
led to the structure we observe. Once, cosmology was often described as
the hunt for two numbers: the rate of expansion (the so-called Hubble constant)
and the density parameter 
(which distinguishes a Universe that will eventually re-collapse from one
that will keep expanding forever). This is no longer true. The field has
seen tremendous progress in the last 20 years and has by now become as
exact as any other field of physics. Theoretical understanding has increased
dramatically, and the amount and accuracy of the data coming through are
now beyond what was considered possible even 5 years ago.
Most of the time, physicists solve (differential) equations that describe
changes in observable quantities (say, temperature or speed) in space and
time. These equations are more or less universal for all areas of physics
and are typically solved for future times starting from knowledge of the
initial state of the system. Cosmology works in a reverse way. We observe
the Universe today, and then one has to extrapolate backwards in time to
figure out the initial conditions and the past history. This is a different
kind of problem and requires different tools.
The Friedman model is generally accepted as an adequate approximation
to the global evolution of the Universe. Its Newtonian interpretation is
simple: the
Universe is homogeneous and expanding in such a way that the expansion
velocity of each shell of cosmic fluid is approximately equal to the escape
velocity from its surface. Such expansion is called the Hubble law, which
states that the relative velocity between any two points is proportional
to the distance between them, v = Hr, H
being the Hubble constant. But one needs Einstein's general theory of relativity
to explain the expansion. Galaxies are attached to fixed (so-called comoving)
coordinates, much like the dots on an inflating balloon, creating the illusion
that they themselves are moving away. The global evolution of such a Universe
is analogous to that of a stone thrown upward. If its speed exceeds the
escape velocity from Earth, the stone will move away forever and eventually
continue its "expansion" without feeling Earth's gravity any
more. If the speed is too small, the stone will expand to a maximum height
and then fall back to Earth and bounce up again. Similarly, if the gravity
of the Universe is strong enough to overcome its expansion, it will reach
a maximum size, turn around, and re-collapse to a singularity, ending its
current cycle in a Big Crunch, and perhaps starting another expansion cycle.
If gravity is too weak, the Universe will continue expanding forever. According
to general relativity, space in the presence of matter is curved, and the
gravity of the matter determines its geometrical properties. In the former
case (re-collapse), the geometry of the Universe is like that of a sphere,
and it is "closed." In the latter case (expansion forever), the
geometry is like that of a saddle, and it is "open." The intermediate
case of precise balance between gravity and escape velocities corresponds
to plane geometry, and is "flat." Figure 1 illustrates the three
possible geometries. The type of universe we live in depends, then, on
the average density and is parameterized by the density parameter ,
which is the ratio of the average density to that necessary to eventually
stop the expansion. If >
1, the Universe is closed, if <
1 it is open, and if =
1, the Universe is flat.
Figure 1 Geometries of flat universe (left), closed
or positive curvature universe (middle), and open or negative curvature
universe (right). The three cases correspond to equal
to, greater than, or less than 1, respectively.
In order to explain bound non-expanding objects (galaxies, clusters
of galaxies, stars, and, ultimately, to some degree ourselves) in an expanding
universe, one has to postulate the existence of (initially) small density
fluctuations imposed on the otherwise homogeneous
expanding fluid. The matter within the fluctuations "sees"
larger mass, feels a stronger gravitational field than the rest of the
Universe, and hence expands at a slower rate. In other words, the density
fluctuation grows with respect to the background. In fact, a good description
of the evolution of fluctuations is to approximate the fluctuation itself
as a mini-universe of a slightly larger density. It will then expand at
a slower rate, reach its maximum expansion stage, and collapse to produce
compact objects. The order and epoch when this happens depend on the spectrum
of the fluctuations - i.e., how the typical amplitude varies with
the scale it contains, on the amplitude of the spectrum, on ,
on the epoch when density fluctuations were introduced, and of what they
consisted.
Even though the expansion of galaxies was discovered by Edwin Hubble
in the 1930's, the Big Bang theory was really placed beyond reasonable
doubt only after the discovery of the microwave background radiation by
Penzias and Wilson in 1964. This is the relic radiation left over from
the Big Bang itself, and is isotropic.
Since the Universe once went through a very hot and very dense phase, this
radiation, via its interactions with hot, dense, and opaque plasma, should
have thermalized to have a blackbody spectrum. Recent measurement by NASA's
Cosmic Background Explorer
(COBE) satellite confirmed this to an unprecedented degree with
measurements from the Far
Infrared Absolute Spectrophotometer (FIRAS) (Figure 2) - few labs
will be able to produce such an accurate blackbody
spectrum! While the radiation was very hot during early phases,
by now it has cooled so much that its peak has (red)shifted into the microwave/radio
region of the spectrum.
![[Image of FIRAS CMB spectrum]](/anima/skash.nsf/filesimg/E4F1BC1028AF472788257377006A7FA9/$File/firas_spectrum.jpg)
Figure
2 Cosmic microwave background (CMB) spectrum from the COBE FIRAS
instrument. The solid curve shows the expected intensity from a single
temperature blackbody spectrum, as predicted by the hot Big Bang theory.
The FIRAS data were taken at 34 positions equally spaced along this curve.
The FIRAS data match the curve so exactly, with error uncertainties less
than the width of the blackbody curve, that it is impossible to distinguish
the data from the theoretical curve. These precise CMB measurements show
that at least 99.994% of the radiant energy of the Universe was released
within the first year after the Big Bang itself. The results show that
the radiation matches the predictions of the hot Big Bang theory to an
extraordinary degree. Credit: NASA's
Goddard Space Flight Center and the COBE Science Working Group.
Click on image to display larger version.
The Universe as we see it poses many questions about the physical laws
responsible for its structure and evolution. One can envisage many laws
that would lead to a very different universe, and some such laws may be
even more logical. For example, there is the
horizon problem: Why is the Universe homogeneous and why does it
have the same appearance on all scales? Signals can propagate only at the
speed of light, c, and this defines the so-called horizon, which
at any given time t, is just ~ct. In the past, this
horizon was very much smaller than it is today. Thus, what could have been
the physical processes that led to different regions of the Universe not
causally connected in the past having the same structure? The luminous
matter in stars and galaxies can account for only 1 percent of the critical
density of the Universe. If that were all the matter there was, it would
have been impossible for small density fluctuations to grow and collapse
into galaxies at all. Luckily, it has been known for some time from the
dynamics of individual galaxies as well as clusters of galaxies that their
total mass is about 10 times larger, which means that the total is
at least 0.1. Galaxies
are surrounded by dark massive halos that contain about 10 times as
much mass as the luminous stars. Thus, the
question of dark matter arises: What is it made of, why, when,
and how much? This, in turn, is related to how big the density of the Universe
really is and whether it will re-collapse or continue expanding forever:
Is it closed, flat, or open? And last but not least, one would like to
understand the
origin of density fluctuations.
Until the early 1980's, cosmologists concentrated mainly on the formation
of structures out of the evolving density fluctuations in the post-recombination
epoch. According to the standard model, the Universe started out of a singularity
with infinite density and infinitely high temperature. The earliest time
when we can start applying the Einstein equations at least semi-confidently
is the so-called Planck era, roughly 10-43 seconds after the
Big Bang. Prior to this time, quantum effects in gravity were dominant,
and the proper treatment of the Universe's evolution has to await creation
of a theory of quantum gravity, one of the still unsolved problems of theoretical
physics. As the Universe expanded, matter cooled, and normal particles
began to appear out of the primordial soup of energy. At about 1-3 minutes
after the Big Bang, the Universe cooled enough for some of the protons
(hydrogen nuclei) to fuse with neutrons thus converting
about 25 percent of the matter into helium and a small, but significant
amount into deuterium or heavy hydrogen. Afterward, matter continued
to cool, but also was so tightly coupled to radiation by electron-photon
scattering that the Universe was opaque and no growth of fluctuations was
possible. When the Universe turned about 105 years old, it cooled
enough that electrons and protons recombined into hydrogen atoms. It became
transparent, and the microwave
background photons began to propagate freely to observers. The
epoch of recombination is the earliest stage in the history of the Universe
that can be observed and studied through observations with photons. This
offers an important tool for studying the early Universe, but also shows
the limitations of how far into its infant stage it can be seen.
Since the early 1980's, theoretical cosmology has seen tremendous -
albeit, at times, speculative - progress. This led to the creation of a
new subfield of astrophysics called astroparticles. As the name suggests,
it resulted from a kind of marriage between astrophysics and high-energy
(particle) physics, and in a way it happened because the Universe offers
the ultimate testing ground for particle physics ideas that cannot be probed
with the current (or even the next) generation of accelerators. The most
popular of these theories is the so-called inflation
theory. According to the standard Big
Bang picture, the Universe decelerates in its expansion because
gravity is the only force driving its evolution. This leads to the horizon
scale increasing linearly with time. However, according to the inflation
theory, at early times not long after the Planck era, the Universe
consisted of a primordial soup of energy, the so-called fields. It was
also inhomogeneous, a more natural initial condition. In the state of equilibrium,
the field would be located at the minimum of the well created by its potential
(just as any physical system tends to the state with minimal energy). According
to current field theories, as the temperature of the Universe decreased,
the form of the field potential changed, and its minimum shifted so that
the field was no longer sitting at its minimum. The field would then start
rolling toward the (new) minimum of the potential well. One can always
expect to find a small region (smaller than the horizon scale at the time)
where the field is distributed homogeneously. If the roll-over is slow
(which sets limits on what the form of the potential can be in order for
inflation to work), wonders can happen in that small homogeneous patch.
The pressure created by such a field during roll-over is dominated by its
potential energy and is equal but opposite in sign to the potential, while
its density (energy) is also dominated by the potential but is equal to
it and has the same sign. Thus, the so-called equation of state during
this process reads: P = -
.
In normal circumstances, the pressure, P, is positive, but during
inflation it is negative and large and, therefore, wins over gravity and
makes the Universe accelerate and expand exponentially - i.e., inflate.
Several things happen during this inflationary
expansion. First, as it expands, the Universe super-cools, and after
the field has reached its new minimal potential and starts oscillating
near the minimum, it decays into normal particles and photons. This re-heats
the Universe, and then the standard Big
Bang picture begins to apply. The second thing that happens during
inflation is that all length scales (including the present horizon) get
stretched exponentially; this means that scales that are not in causal
contact today could have been so before inflation (when they were much
more compact). The homogeneity
and the horizon
problem are thus explained by supposing that the entire observable
Universe originated from this initial bubble that was inflated.
As the field rolls down the potential curve, new fluctuations will appear
due to quantum uncertainty effects. These fluctuations have the so-called
scale invariant Harrison-Zeldovich spectrum; i.e., the amplitude
of energy fluctuations on a given scale is independent of the scale. There
are some problems vis-a-vis field theories, however. One can show that,
for the density fluctuations produced to be as small as required by the
homogeneity of the Universe, the field potential must have a very small
coupling constant. Last but not least, inflation predicts that, during
this roll-over, the Universe becomes very nearly flat, driving the density
parameter very
close to 1. All of these are testable
predictions.
There are also a few alternative theories. Some are based on the topological
defects that can appear in space-time during phase transition(s) in the
early Universe. These would lead to exotic first objects such as strings,
textures, or domain walls, all of which are defects in the otherwise homogeneous
space-time. These serve as the seeds for density fluctuations whose later
evolution leads to the observed structures. And last, but not least, low
values of can
be reconciled with standard inflationary picture if the total density is
dominated by the vacuum
energy - the so-called cosmological
constant 
-
thereby ensuring that the space-time is flat.
All of these theories make predictions about the present-day Universe
that can be checked. The strongest (and perhaps most problematic) prediction
of the standard inflationary picture is that the Universe today should
be flat to a high accuracy. This makes a prediction on what
the dark matter should be made of. The nucleosynthesis
calculations (helium, deuterium, and lithium production) set strong
limits on what the density in normal, so-called baryonic matter (protons
and neutrons) can be. Deuterium cannot be made in significant amounts by
any known processes other than the Big Bang, and it is, therefore, a particularly
sensitive indicator of the total baryon density. Deuterium abundance measured
in the Solar System and now also in interstellar clouds by the Keck
and Hubble telescopes implies
that the density of baryons
can not exceed ~10 percent of the closure
density. This, in turn, means that for inflation to work with the
total density of the Universe at the critical value, the dominant bulk
of matter in the Universe (~90 percent) must be in some non-baryonic form.
One such candidate is neutrinos,
whose number density is known from the theory of weak interactions and
the physics of the early Universe. The idea that neutrinos may be massive
has recently received support from the Kamiokande
measurements of the cosmic ray spectra that measured mass difference between
the various neutrino species. The measurements indicated that the difference
in masses is about 0.01 eV. This certainly suggests that the neutrino is
indeed a massive particle, requiring revision of the standard model of
particle physics. On the other hand, for neutrinos to be "minimally"
cosmologically important they need to have mass in excess of a few eV,
which is significantly larger than their mass difference. In order to make
the Universe flat, they then must have mass of about 30 eV (for comparison,
the mass of an electron is 500,000 eV), but this hypothesis is not easy
to reconcile with the formation of the observed structures. Thus, some
physicists speculate that the dominant mass of the Universe is in some
new exotic form - the so-called Cold
Dark Matter. Many experiments are now underway to detect this hypothetical
new matter, and many theories are being put forward that predict the new
particles' form, interactions, and masses.
There are several possible ways to measure .
The most obvious way is to weigh the matter in the Universe - at least
the luminous part of it that is concentrated in galaxies and clusters of
galaxies. The dynamics of the latter allows us to determine their masses
assuming (quite reasonably) that these systems are in equilibrium between
gravity and pressure due to centrifugal forces or random motions. (Note
that this is also the way the mass of Earth is determined from the Moon's
motion, etc.). Such
measurements were pioneered by Zwicky in the 1930's, and have since
consistently given a value of =
0.1 - 0.2. This is about 10 times as much as the luminous mass density
(so there definitely is dark
matter), but a factor of 10 below the critical
density so that the dark
matter associated with galaxies is not enough to make the Universe
flat. Thus, either inflation
theory is in trouble, or there must be about 10 times as much matter
as we have been able to detect. But where could it be?
Or do we live in a low density Universe whose density is dominated by
the vacuum
energy component, the cosmological constant ?
Indeed support for such a scenario comes from recent measurements of supernovae
of type Ia at (high) redshifts out to z ~ 1. Type Ia
supernovae form due to catastrophic nuclear burning by matter falling onto
the surfaces of already-formed white dwarf stars. Because white dwarfs
have mass specified by the Chandrasekhar limit, 1.44 MSun, these
supernovae represent "standard candles," i.e., they all
have very similar luminosities at the peak of their explosion, and similar
light curves, which describe how the luminosity emitted by the exploding
star varies as a function of time since the explosion. Thus, one can derive
the distance to a Type Ia supernova from its apparent brightness.
Such distances for supernovae at redshifts z > 0.5 are sensitive
to the cosmological parameters and
, enabling measurement
of the latter. Several groups have recently detected enough Type Ia
supernovae in this range of redshifts to give the first reliable measurements
of the cosmological parameters. Although the present-day measurements have
large uncertainties, the available data seem to favor a low density Universe
dominated by the cosmological
constant. If confirmed with future and larger datasets, this would
have profound implications for cosmology. It is expected that quantum
uncertainty in the state of the early Universe could generate a
cosmological constant whose magnitude is comparable to the Planck
mass energy. But the data and the fact that the Universe is at
least 10 billion years old suggest that the observed value of the cosmological
constant is more than 120 orders of magnitude lower than that.
So how could it have been generated with values so small, yet different
from zero?
The other test of is
by measuring the age
of the Universe. Obviously, it must be at least as old as the oldest
systems it contains. Such systems are thought to be globular clusters of
stars for which age determinations make the Universe at least 14 - 17 billion
years old. Theoretically, one can predict what the age of the Universe
is if one knows H, and
. If =
0 and gravity is negligible (
<< 1), there is little deceleration, and the
age would be H-1, the so-called Hubble time, but
if = 1, the age
is decreased by a factor of 2/3. Two recent measurements
of H from the Hubble Space Telescope and the Keck
telescope on Mauna Kea in Hawaii lead to H-1
~ 13 billion years. If =
1, the age implied by this expansion rate would be significantly smaller
than the age of globular clusters. Is the Universe open after all? If so,
can the inflationary
model be modified to account for this? A non-zero positive cosmological
constant would also lead to an increase in the age of the Universe
for a given value of the Hubble constant (H) and could lead to an
age even in excess of the Hubble time, H-1.
The other key test of theories
of galaxy formation is the spectrum of density fluctuations and how
early in the Universe they were imprinted. As mentioned, one can hope to
see only as far as the epoch of recombination. This would still correspond
to seeing the Universe when it was only 150,000 years old, or roughly one
hundred thousandth of its present age! According to the conventional wisdom,
no stars yet existed
at that time, but small density fluctuations that were later to lead
to galaxies had already been put in place. Microwave
background photons last interacted with matter at the onset of recombination
and, therefore, should carry memory of what the density in the Universe
looked like then. In a seminal paper in 1965, shortly after the discovery
of the microwave background, two theoreticians, Sachs and Wolfe, showed
that the slightly inhomogeneous gravitational field generated by density
fluctuations, if already present then, should lead to very small temperature
fluctuations in the microwave background. Their amplitude should be
very tiny - about 1 part in 10,000 to 100,000 in the relative temperature
differences on scales separated by several degrees (or more) on the sky.
Hence, the searches for these anisotropies
began very soon after the microwave background was discovered.
Figure
3 Spectra of the Galactic foreground emission components (free-free,
synchrotron and dust) and the cosmic microwave background. The COBE DMR
bands were strategically located in the region of minimum foreground emission,
at 31.5, 53, and 90 GHz. Credit: C. Bennett (see Bennett
et al. 1992, Astrophysical Journal, 396, L7).
Click on image to display larger version.
Figure 3 illustrates how difficult it is to measure these anisotropies.
The radiation peaks at frequency of about 5 cm-1 or 150 GHz.
Since one observes it through the "smog" of our Galaxy, in order
to find the tiny fluctuations, one has to eliminate the contributions from
the Galaxy to a very high degree of accuracy. The task of measuring anisotropies
from the ground is further frustrated by the effects of Earth's atmosphere.
Thus, despite persistent attempts, no convincing evidence came for almost
three decades. Then, in 1989, NASA launched the COBE
satellite with the explicit task of measuring the microwave background
sky from above the atmosphere. COBE
had three instruments: the above-mentioned FIRAS
to measure the spectrum of the microwave background very accurately, the
Differential
Microwave Radiometers (DMR) to measure the anisotropies, and the
COBE
DMR was designed to operate in the range of wavelengths where the
foregrounds, coming from the free-free and synchrotron emission at short
frequencies and from Galactic dust at long frequencies, have minimal pollution.
In April 1992, at the American Physical Society meeting in Washington,
DC, the COBE team
announced the discovery of anisotropies at the level of about 1 part in
100,000 on a scale of a few degrees. The angular spectrum of the anisotropies
is consistent with the inflationary theory, but within uncertainties it
is also consistent with the predictions of its competitors. Figure 4 shows
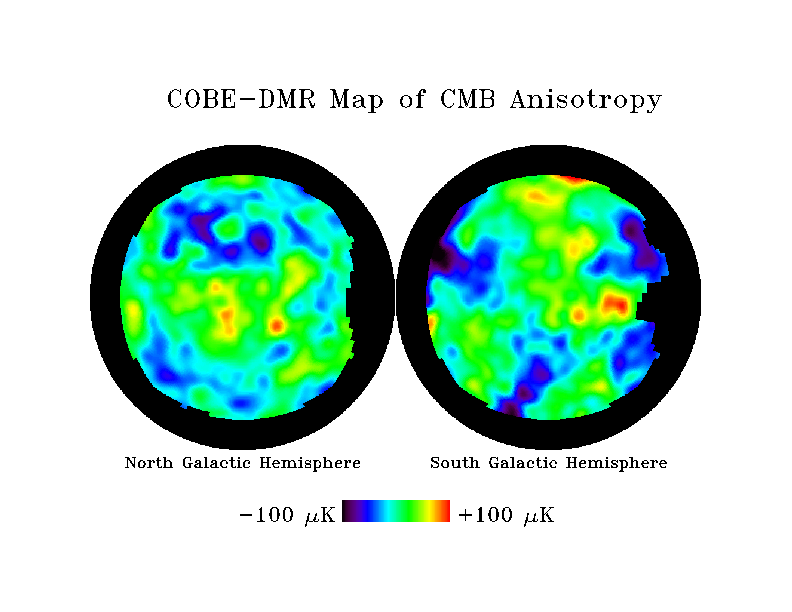
the microwave background sky as seen by the DMR.
What was measured and is shown is nothing less than the entire observable
Universe when it was only approximately 105 years old.
![[Image of DMR data]](dmr_4yr_cmb_stereo_wallet.gif)
Figure
4 This false-color image shows tiny variations in the intensity of
the cosmic microwave background measured in four years of observations
by the DMR instrument on NASA's COBE satellite. The blue and
red spots correspond to regions of greater or lesser density in the early
Universe. These "fossilized" relics record the distribution of
matter and energy in the early Universe before the matter became organized
into stars and galaxies. The features traced in this map stretch across
the visible Universe: the largest features seen by optical telescopes,
such as the "Great Wall" of galaxies, would fit neatly within
the smallest feature in this map. Credit: NASA's
Goddard Space Flight Center and the COBE Science Working Group.
Click on image to display larger version.
The third COBE instrument
- DIRBE
- detected the Cosmic Infrared Background (CIB) at wavelengths
of 140 and 240 µm (micrometers), and set limits to the CIB brightness
at eight other infrared wavelengths ranging from 1.25 to 100 µm.
CIB emission was also seen at the highest frequencies observed in the COBE FIRAS spectra,
providing independent confirmation of the DIRBE result.
The (high) levels of the cosmic infrared background at long infrared wavelengths
are probably indicative of early galaxy formation and efficient dust production
in high-redshift galaxies. These results have profound implications for
cosmology and the physics of galaxy formation. As illustrated in Figure
5, foreground infrared
emission from the solar system (zodiacal light)
and the Milky Way had to be modeled accurately and subtracted from the
observed sky brightness in order to find the cosmic infrared background.
Figure
5 Cosmic Infrared Background emission was detected in data from the
COBE Diffuse Infrared Background Experiment. The map at the top is
a false-color image showing the observed infrared sky brightness at wavelengths
of 60 (blue), 100 (green) and 240 µm (red). The bright white-yellow
horizontal band across the middle of the image corresponds to emission
from interstellar dust in the plane of our Milky Way Galaxy (the center
of the Galaxy lies at the center of the map). The red regions above and
below this bright band are "infrared cirrus" clouds, wispy clouds
of relatively cool Galactic dust. The blue S-shaped figure follows the
ecliptic plane and represents emission from interplanetary dust in the
solar system. The map in the middle is a 60-100-240 µm false-color
image depicting the sky after the foreground glow of the interplanetary
dust has been modeled and subtracted; this image is dominated by emission
from interstellar dust in the Milky Way. After the infrared light from
our solar system and Galaxy has been removed, what remains is a
uniform Cosmic Infrared Background. This is illustrated in the bottom image,
which shows just the residual 240 µm brightness. The line across
the center is an artifact from removal of the Galactic light. Credit: STScI
OPO - PRC98-01; M. Hauser and NASA.
Click on image to display larger version.
Last but not least, the recent years have seen a dramatic observational
breakthrough that can perhaps offer a clue to the nature of dark
matter. As mentioned, the only place we know that dark matter should
definitely exist is in the galactic halos, including the halo of our Galaxy.
This dark matter can consist either of elementary particles (neutrinos,
cold dark
matter) or dark astronomical objects. These objects can either
have a very low (sub-stellar) mass of ~0.1 solar masses, in which case
they are called brown dwarfs or "Jupiters," or be massive black
holes. From Galactic dynamics, we know that if they are very massive, their
mass must be less than about 106 solar masses, because more
massive objects would sink to the center of our Galaxy in less than its
age due to dynamical friction, contrary to what is observed. But what if
they are low-mass "Jupiters"? In this case, micro-lensing can
offer a way to find these objects if dark matter is composed largely of
them. According to general relativity, a gravitating body deflects light
and acts like an optical lens. Then, because of the focusing, it leads
to greater luminosity of the lensed object (more photons are now focused
on the observer). Suppose now that we are looking at stars in other galaxies
through the halo of our own. Because any Jupiters in the halo must be moving
(just like stars in the galaxies), every now and then they would pass between
the monitored star and us, resulting in a sudden flare-up in the apparent
brightness of the background star. From the intensity and duration of the
flash, one can derive the mass of the passing dark object. Such events
should be very rare for any given star, but if the halo contains many Jupiters,
then by monitoring a few million
stars in the Small and Large Magellanic Clouds, which are satellites
of our Galaxy, one expects to see several such events
per year. Two things distinguish such amplification from intrinsic variability.
First, the detected event must be achromatic, i.e. wavelength independent.
Second, the flash must be strictly symmetrical in time. Three groups of
collaborating astronomers and particle physicists have now discovered such
events. One, dubbed the "Gold Plated Event," was caused by an
object whose mass is about one-tenth that of the Sun. Could it be that
dark matter
is composed predominantly of "Jupiters" as the most recent analysis
of the combined data seems to suggest? Time will tell.
![[Blue bullet]](blu_bullet.gif)
COBE Educational Resources
COBE
Home Page
NASA Rep. and editor David Leisawitz,
leisawitz@stars.gsfc.nasa.gov
Last Revised 25 August 1998